Divisibilidad

En matemáticas, concretamente en aritmética, se dice que un número entero b es divisible entre otro entero a (no nulo) si existe otro entero c tal que: ${displaystyle b=acdot c}$. Esto es equivalente a decir que el resto de la división euclídea es cero o simbólicamente ${displaystyle b-acdot c=0}$.

Se suele expresar de la forma ${displaystyle amid b}$, que se lee: «a divide a b», o «a es un divisor de b» o también «b es múltiplo de a».^[1]​ Por ejemplo, 6 es divisible entre 3, ya que 3×2=6; pero 6 no es divisible entre 4, pues no existe un entero c tal que 4×c=6; es decir que el resto de la división euclídea (entera) de 6 entre 4 no es cero.

Cualquier número natural^[2]​ es divisible entre 1 y entre sí mismo. Los números mayores que 1 que no admiten más que estos dos divisores se llaman números primos. Los que admiten más de dos divisores se llaman números compuestos.

El número entero ${displaystyle a}$ es divisible entre el número entero ${displaystyle b eq 0}$ (o lo que es lo mismo, b divide a a) si hay un número ${displaystyle q}$ entero, tal que ${displaystyle a=bcdot q}$.

Este hecho se denomina divisibilidad del número entero ${displaystyle a}$ por el número entero ${displaystyle b}$ y se denota por ${displaystyle b|a}$; que no es otra cosa que una afirmación entre los números enteros, que, en un contexto concreto, puede ser cierta o no.^[3]​ Por ejemplo ${displaystyle 3|12}$ es cierta; sin embargo, ${displaystyle 3|17}$ no es cierta. Si ${displaystyle b}$ no es divisor de ${displaystyle a}$ se escribe ${displaystyle b mid a}$. Nótese que ${displaystyle 0 mid a}$ para todo ${displaystyle a}$ distinto de cero, pues ${displaystyle a eq 0=kcdot 0}$ para todo ${displaystyle k}$ entero.

Se denomina factor o divisor propio de un número entero n, a otro número también entero que es divisor de n, pero diferente de 1 y de n. Los divisores 1 y n son denominados impropios.

Por ejemplo, los divisores propios de 28 son 2, 4, 7 y 14. Cuando se toman en cuenta enteros negativos, un divisor propio es aquel cuyo valor absoluto es menor que el número dado. En este caso, los divisores propios serían -14, -7, -4, -2, 2, 4, 7, 14.

Casos especiales: 1 y -1 son factores triviales de todos los enteros, y cada entero es divisor de 0. Los números divisibles por 2 son llamados pares y los que no lo son se llaman impares.

Si d es un divisor de a y el único divisor que admite d es 1 y él mismo, se llama divisor primo de a. De hecho es un número primo. El 1 es el único entero que tiene un solo divisor positivo.

Sean ${displaystyle a,b,cin mathbb {Z} }$, es decir ${displaystyle a}$, ${displaystyle b}$ y ${displaystyle c}$ son números enteros. Se dan las propiedades básicas:

Si la factorización en números primos de n viene dada por

entonces el número de divisores positivos de n es

y cada uno de los divisores tiene la forma

donde ${displaystyle 0leq mu _{i}leq u _{i}}$ para cada ${displaystyle 1leq ileq k.}$^[7]​

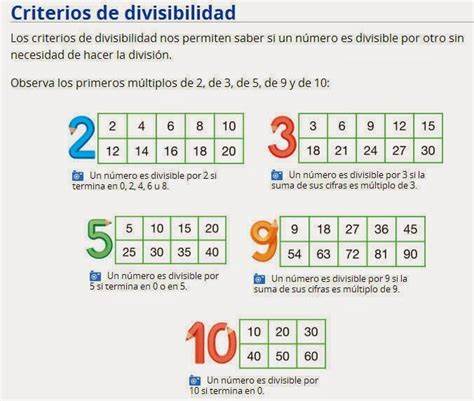
Los siguientes criterios permiten averiguar si un número es divisible entre otro de una forma sencilla, sin necesidad de realizar la división.

Otro sistema: Si la suma de la multiplicación de los números por la serie 2,3,1,-2,-3,-1... da 0 o un múltiplo de 7.

Ejemplo método 2: 34349: (2*3+3*4+1*3-2*4-3*9)= 6+12+3-8-27 = -14. ^[8]​

Si el número tiene solo dos cifras y estas son iguales será múltiplo de 11.

66: porque las dos cifras son iguales. Entonces 66 es múltiplo de 11.

4250: Este número también sería divisible entre 125 ya que sus tres últimas cifras son múltiplo de 125.

Nota 1: Existen muchas versiones de los criterios de divisibilidad. Así por ejemplo, para el 13 resulta equivalente el criterio: al separar la última cifra de la derecha, multiplicarla por 4 y sumarla a las cifras restantes la suma es igual a 0 o es un múltiplo de 13.

Nota 2: Resulta curioso que el criterio de divisibilidad por 7 sirva también como criterio de divisibilidad por 3, aunque evidentemente el criterio tradicional resulta más sencillo y este no se utiliza: al separar la última cifra de la derecha, multiplicarla por 2 y restarla de las cifras restantes la diferencia es igual a 0 o es un múltiplo de 3.

Nota 3: Aunque existen criterios similares para cualquier número primo, con frecuencia resulta más sencillo dividir que aplicar un criterio complicado (como el del 13). Sin embargo existe un criterio general que funciona siempre y que en muchos casos es suficientemente práctico: restar el número primo (o múltiplos de este) a las cifras de la izquierda sucesivamente hasta obtener cero o ese número primo. Así el ejemplo del 13 se podría comprobar con el proceso siguiente (usamos el 39 =3*13 para abreviar pasos): 3822 (restamos 13 dos veces a la izquierda) → 2522 → 1222 (restamos 39 tres veces de las tres cifras de la izquierda) → 832 → 442 → 52 y al restar de nuevo 39 obtenemos 52-39 =13

Nota 4: El método no tiene que ceñirse solo al proceso de quitar las unidades. Pueden quitarse unidades y decenas. Así por ejemplo: 201 es múltiplo de 67. Un criterio para el 67 sería: quitamos el número formado por las decenas y unidades y se lo restamos 2 veces a las cifras que quedan, si el resultado es múltiplo de 67, el número anterior también lo será. Ejemplo: 66129, hacemos 661-2·29=603, Ahora 6 -2·3=0, luego 66129 es múltiplo de 67.

Una prueba de esto es la siguiente: (N-d)/100-2d = (N-d-200d)/100 = (N - 201d)/100= k. Si k es múltiplo de 67, N también lo será puesto que N = 100k+201d.

Nota 5: Para saber si un número de 3 cifras es múltiplo de 8. Hay que tener en cuenta lo siguiente: Si la cifra de las centenas es par y las otras 2 es un múltiplo de 8 (288→ 2 es cifra par, y 88 múltiplo de 8) o si la cifra de las centenas es impar y las dos últimas son el resultado de la diferencia o suma de un múltiplo de 8 con 4 (168→ 1 es cifra impar y 68+4=72; 72 es múltiplo de 8.

Nota 6: Todo número de tres cifras, en el cual las tres cifras son iguales, es múltiplo de 3 y de 37; de hecho es la multiplicación de 37 por la suma de sus cifras. Ejemplo: 333 es múltiplo de 37, porque 333=37*9 (3+3+3=9).

Todos los criterios señalados funcionan si el número está escrito en el sistema de numeración decimal. En otra base no siempre ocurre así. Pues 102₇, escrito en base 7, termina en cifra par, pero no es divisible entre 2. En este caso se suman las cifras 1+2=3; 3=1 (Mód 2), luego 102₇ es impar (en decimal es 7²+2=51).

La divisibilidad es posible tratar dentro de la propiedades aritméticas de los

---