Distribución chi cuadrado

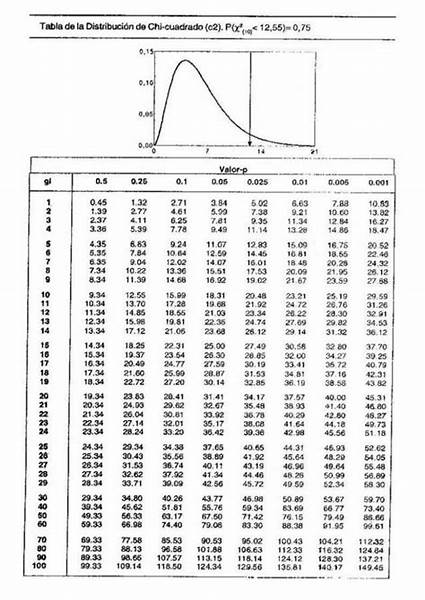
En teoría de la probabilidad y en estadística, la distribución ji al cuadrado (también llamada distribución de Pearson o distribución ) con grados de libertad es la distribución de la suma del cuadrado de variables aleatorias independientes con distribución normal estándar. La distribución chi cuadrada es un caso especial de la distribución gamma y es una de las distribuciones de probabilidad más usadas en Inferencia Estadística, principalmente en pruebas de hipótesis y en la construcción de intervalos de confianza.
Sean variables aleatorias independientes tales que para entonces la variable aleatoria definida por
tiene una distribución chi cuadrada con grados de libertad.
Si la variable aleatoria continua tiene una distribución Chi Cuadrada con grados de libertad entonces escribiremos o .
Si entonces la función de densidad de la variable aleatoria es
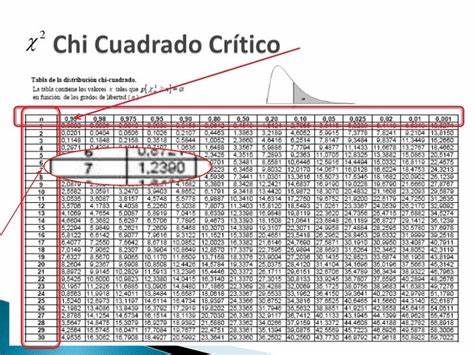
para donde es la función gamma.
Si entonces su función de distribución está dada por
donde es la función gamma incompleta.
En particular cuando entonces esta función toma la forma
Si entonces la variable aleatoria satisface algunas propiedades.
La media de la variable aleatoria es
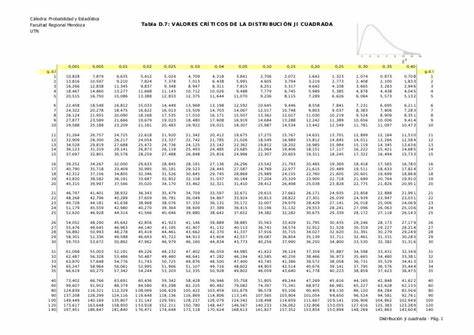
La varianza de la variable aleatoria es
La función generadora de momentos de es
para .
Sea una muestra aleatoria proveniente de una población con distribución entonces
donde
y
son la media y varianza de la muestra aleatoria respectivamente.
Sean una muestra aleatoria proveniente de una población con distribución donde y son desconocidos.
Se tiene que
Sean tales que
siendo entonces
por lo tanto un intervalo de de confianza para está dado por
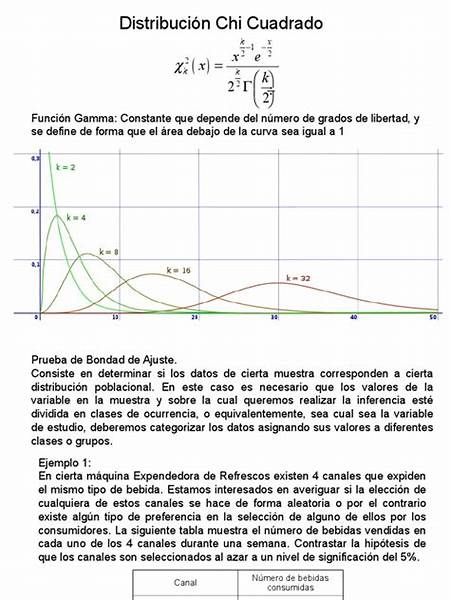
La distribución χ² tiene muchas aplicaciones en inferencia estadística. La más conocida es la denominada prueba χ², utilizada como prueba de independencia y como prueba de buen ajuste y en la estimación de varianzas. Pero también está involucrada en el problema de estimar la media de una población normalmente distribuida y en el problema de estimar la pendiente de una recta de regresión lineal, a través de su papel en la distribución t de Student.
Aparece también en todos los problemas de análisis de varianza por su relación con la distribución F de Snedecor, que es la distribución del cociente de dos variables aleatorias independientes con distribución χ².
Véase esto también
Escribe un comentario o lo que quieras sobre Distribución chi cuadrado (directo, no tienes que registrarte)
Comentarios
(de más nuevos a más antiguos)
Aún no hay comentarios, ¡deja el primero!




















