Distribución de Poisson

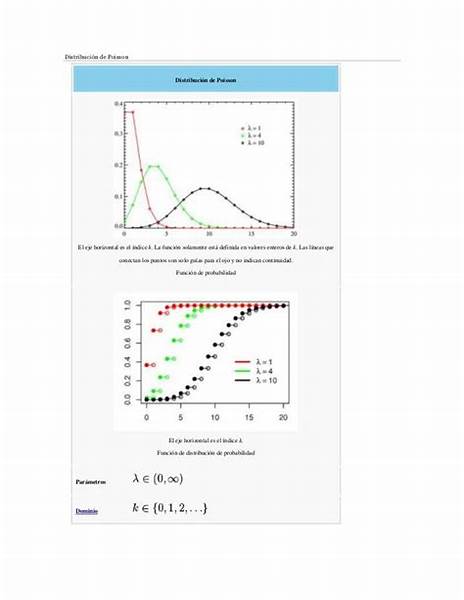
En teoría de probabilidad y estadística, la distribución de Poisson es una distribución de probabilidad discreta que expresa, a partir de una frecuencia de ocurrencia media, la probabilidad de que ocurra un determinado número de eventos durante cierto período de tiempo. Concretamente, se especializa en la probabilidad de ocurrencia de sucesos con probabilidades muy pequeñas, o sucesos «raros».

Fue propuesta por Siméon-Denis Poisson, que la dio a conocer en 1838 en su trabajo Recherches sur la probabilité des jugements en matières criminelles et matière civile (Investigación sobre la probabilidad de los juicios en materias criminales y civiles).

La distribución de Poisson es popular porque modela el número de veces que ocurre un evento en un intervalo de tiempo.

Sea ${displaystyle lambda >0}$ y ${displaystyle X}$ una variable aleatoria discreta, si la variable aleatoria ${displaystyle X}$ tiene una distribución de Poisson con parámetro ${displaystyle lambda }$ entonces escribiremos ${displaystyle Xsim operatorname {Poisson} (lambda )}$ o ${displaystyle Xsim operatorname {Poi} (lambda )}$.

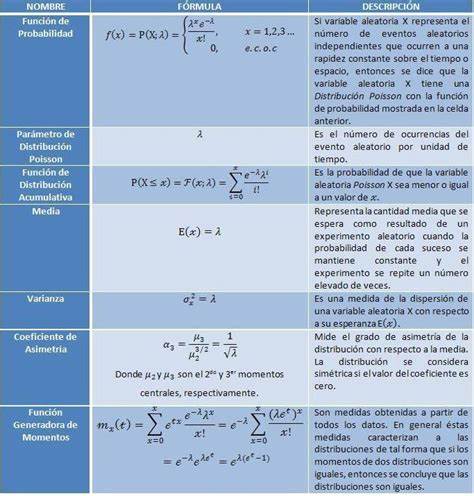
Si ${displaystyle Xsim operatorname {Poisson} (lambda )}$ entonces la función de probabilidad es

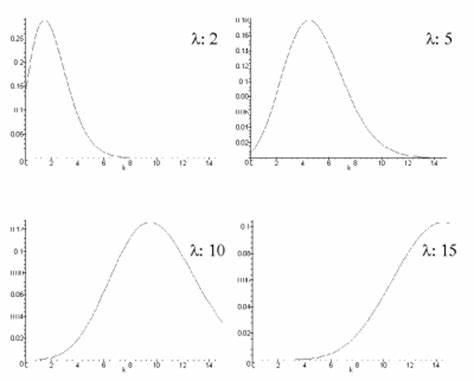
donde ${displaystyle k=0,1,2,dots }$ es el número de ocurrencias del evento o fenómeno.

El parámetro ${displaystyle lambda >0}$ representa el número de veces que se espera que ocurra dicho fenómeno durante un intervalo dado. Por ejemplo, si el suceso estudiado tiene lugar en promedio 4 veces por minuto y estamos interesados en la probabilidad de que ocurra ${displaystyle k}$ veces dentro de un intervalo de 10 minutos, usaremos un modelo de distribución de Poisson con λ = 10×4 = 40.

En ocasiones, para calcular las probabilidades, se utiliza la siguiente fórmula recursiva para calcular ${displaystyle operatorname {P} [X=k+1]}$ en términos de ${displaystyle operatorname {P} [X=k]}$

por lo tanto

siempre que ${displaystyle operatorname {P} [X=k] eq 0}$.

Si ${displaystyle Xsim operatorname {Poisson} (lambda )}$ entonces la variable aleatoria ${displaystyle X}$ satisface algunas propiedades.

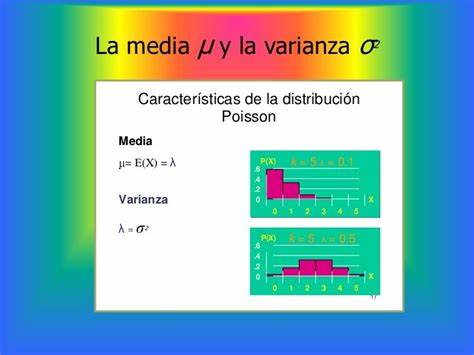
La media de la variable aleatoria ${displaystyle X}$ es

Esta se demuestra por definición de esperanza matemática

La varianza de la variable aleatoria ${displaystyle X}$ es

Es decir, tanto el valor esperado como la varianza de una variable aleatoria con distribución de Poisson son iguales a ${displaystyle lambda }$.

Los momentos de orden superior son polinomios de Touchard en ${displaystyle lambda }$ cuyos coeficientes tienen una interpretación combinatoria. De hecho, cuando el valor esperado de la distribución de Poisson es 1, entonces según la fórmula de Dobinski, el ${displaystyle n}$-ésimo momento iguala al número de particiones de tamaño ${displaystyle n}$.

La moda de la variable aleatoria ${displaystyle X}$ es

esto es, el mayor de los enteros menores que ${displaystyle lambda }$ (los símbolos ${displaystyle scriptstyle lfloor floor }$ representan la función parte entera).

La función generadora de momentos de la distribución de Poisson está dada por

Las variables aleatorias de Poisson tienen la propiedad de ser infinitamente divisibles.

La divergencia Kullback-Leibler desde una variable aleatoria de Poisson de parámetro ${displaystyle lambda _{0}}$ a otra de parámetro ${displaystyle lambda }$ es

Un criterio fácil y rápido para calcular un intervalo de confianza aproximada de ${displaystyle lambda }$ es propuesto por Guerriero (2012).^[1]​ Dada una serie de eventos k (al menos el 15-20) en un periodo de tiempo T, los límites del intervalo de confianza para la frecuencia vienen dadas por:

entonces los límites del parámetro ${displaystyle lambda }$ están dadas por:${displaystyle lambda _{low}=F_{low}T;lambda _{upp}=F_{upp}T}$.

La suma de variables aleatorias de Poisson independientes es otra variable aleatoria de Poisson cuyo parámetro es la suma de los parámetros de las originales. Dicho de otra manera, si

son N variables aleatorias de Poisson independientes, entonces

La distribución de Poisson es el caso límite de la distribución binomial. De hecho, si los parámetros n y ${displaystyle heta }$ de una distribución binomial tienden a infinito (en el caso de n) y a cero (en el caso de ${displaystyle heta }$) de manera que ${displaystyle lambda =n heta }$ se mantenga constante, la distribución límite obtenida es de Poisson.

Como consecuencia del teorema central del límite, para valores grandes de ${displaystyle lambda }$, una variable aleatoria de Poisson X puede aproximarse por otra normal dado que el cociente

converge a una distribución normal de media 0 y varianza 1.

Supóngase que para cada valor t > 0, que representa el tiempo, el número de sucesos de cierto fenómeno aleatorio sigue una distribución de Poisson de parámetro λt. Entonces, los tiempos transcurridos entre dos sucesos sucesivos sigue la distribución exponencial.

Si el ${displaystyle 2\%}$ de los libros encuadernados en cierto taller tienen encuadernación defectuosa, para obtener la probabilidad de que ${displaystyle 5}$ de ${displaystyle 400}$ libros encuadernados en este taller tengan encuadernaciones defectuosas usamos la distribución de Poisson, si se define ${displaystyle X}$ como el número de libros que tengan encuadernación defectuosa entonces ${displaystyle k=5}$ y ${displaystyle lambda }$ (el valor esperado de libros defectuosos) es el ${displaystyle 2\%}$ de ${displaystyle 400}$, es decir, ${displaystyle 8}$. Por lo tanto, la probabilidad buscada es:

La distribución de Poisson se aplica a varios fenómenos discretos de la naturaleza (esto es, aquellos fenómenos que ocurren 0, 1, 2, 3,etc. veces durante un periodo definido de tiempo o en un área determinada y con un número definido de grados de libertad) cuando la probabilidad de ocurrencia del fenómeno es constante en el tiempo o el espacio. Ejemplos de estos eventos que pueden ser modelados por la distribución de Poisson incluyen: