Mínimo común múltiplo

En matemáticas, el mínimo común múltiplo (abreviado m.c.m.) de dos o más números naturales es el menor múltiplo común de todos ellos (o el divisor del conjunto de los múltiplos comunes del divisor ). Este concepto ha estado ligado históricamente con números naturales, pero se puede usar para enteros negativos o número complejo.

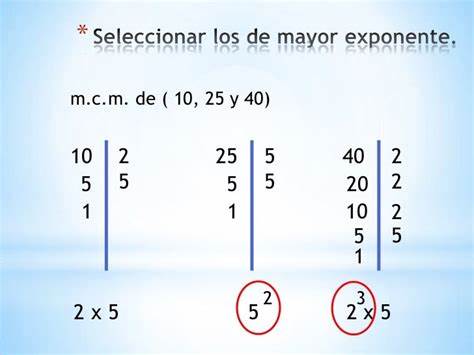
Partiendo de dos o más números y por descomposición en factores primos, expresados como producto de factores primos, su mínimo común múltiplo será el resultado de multiplicar todos los factores comunes y no comunes elevados a la mayor potencia, por ejemplo el mcm de 72 y 50 será

Tomando los factores con su mayor exponente, tenemos que:

Conociendo el máximo común divisor de dos números, se puede calcular el mínimo común múltiplo de ellos, que será el producto de ambos dividido entre su máximo común divisor.

El mcm se puede emplear para sumar o restar fracciones de distinto denominador, tomando el mcm de los denominadores de las fracciones, y convirtiéndolas en fracciones equivalentes que puedan ser sumadas. Véase el siguiente ejemplo:

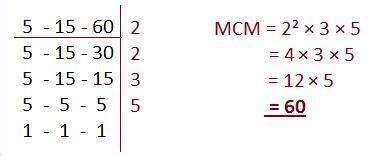
Para poder efectuar la suma, primero se debe buscar el mínimo común múltiplo de los denominadores (6 y 33)

luego el mínimo común múltiplo de 6 y 33 es:

que corresponde al número 66; ambas fracciones tendrán como denominador 66, ahora solo hay que hallar a cada fracción su fracción equivalente, con denominador 66 y será posible la suma:

operando las fracciones, podemos realizar la suma:

El m.c.m. para dos expresiones algebraicas coeficiente numérico y de menor grado que es divisible exactamente por cada una de las expresiones dadas. Esta teoría es de suma importancia para las fracciones y ecuaciones.^[6]​

De esta forma el m.c.m. de monomios ${displaystyle 4a}$ y ${displaystyle 6a^{2}}$ es ${displaystyle 12a^{2}}$ igualmente para ${displaystyle 2x^{2}, 6x^{3}}$ y ${displaystyle 9x^{4}}$ es ${displaystyle 18x^{4}}$.

Para más de dos números, un algoritmo es el siguiente:

Por ejemplo, calculando el mcm(324,16,7,5) La descomposición de 324 es 2²·3⁴; la descomposición de 16 es: 2⁴; la descomposición de 7 es 7 y la descomposición de 5 es 5.

Por tanto, obtenemos el mcm: 2⁴·3⁴·7·5 = 45360.

El concepto de m.c.m. y de m.c.d. se puede extender a las fracciones o números racionales positivos.^[7]​ Estrictamente hablando cualquier número racional divide a otro racional y no existe un racional mayor o menor que todos. No obstante, la extensión aquí descrita tiene interés en algunos problemas y está relacionada con la teoría de anillos, ideales, identidad de Bézout, teorema de Krull, etc.

En el caso de la aritmética clásica elemental sería de aplicación en el siguiente ejemplo. Sean 3 corredores dando vueltas a un circuito, si en cada vuelta el primero saca 1/3 de vuelta al segundo y 2/7 al tercero. ¿cuándo volverán a coincidir en la meta los tres corredores?. También sería de aplicación en problemas de ruedas dentadas, etc.

Sean dos fracciones ${displaystyle {frac {a}{b}}}$ y ${displaystyle {frac {c}{d}}}$ irreducibles

${displaystyle a=prod _{i}p_{i}^{e_{i}(a)},b=prod _{i}p_{i}^{e_{i}(b)},c=prod _{i}p_{i}^{e_{i}(c)},d=prod _{i}p_{i}^{e_{i}(d)}}$

La descomposición en factores primos de ${displaystyle a,b,c,d}$. Entonces

es una fracción que es común múltiplo de ${displaystyle {frac {a}{b}}}$ y ${displaystyle {frac {c}{d}}}$ y es el mínimo por las propiedades del m.c.m. y m.c.d. de dos enteros no negativos ya que ${displaystyle {prod _{i}p_{i}^{max(e_{i}(a),e_{i}(c))}}}$ es el m.c.m. de los numeradores y ${displaystyle {prod _{i}p_{i}^{min(e_{i}(b),e_{i}(d))}}}$ es el m.c.d. de los denominadores de manera que se puede concluir que

Análogamente o teniendo en cuenta que el producto de dos números es igual al de su m.c.m. por su m.c.d. obtenemos:

Las fórmulas anteriores son válidas para una cantidad finita de fracciones. Además el cociente del mcm entre cada fracción es un entero y el conjunto de los cocientes forman un sistema de primos entre sí. De igual manera, el cociente de cada fracción entre el mcd es entero, los cocientes son primos entre sí^[8]​

De manera más general, concepto de m.c.m. tiene sentido en cualquier dominio entero. Mayor uso se da en el conjunto de los enteros, polinomios en una variable, enteros gaussianos^[9]​

---