Prisma (geometría)

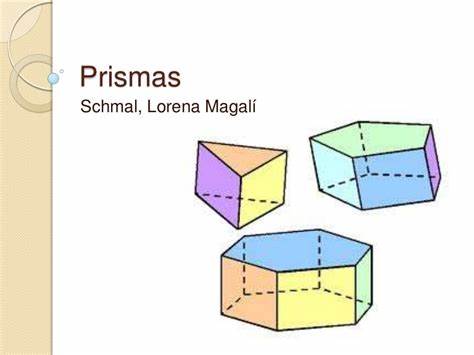
Un prisma, en geometría, es un poliedro que consta de dos caras iguales y paralelas llamadas bases, y de caras laterales que son paralelogramos. Los prismas se nombran por la forma de su base, por lo que un prisma de base pentagonal se llama prisma pentagonal.^[1]​ Los prismas son una subclase de los prismatoides.

Un prisma es un poliedro que cumple las siguientes dos propiedades:

Un prisma recto es un prisma en el que los bordes de unión y las caras son perpendiculares a las caras de la base. Esto se aplica si las caras de unión son rectangulares. Si los bordes de unión y las caras no son perpendiculares a las caras de la base, se llama prisma oblicuo.

Algunos textos pueden aplicar el término de prisma rectangular o prisma cuadrado tanto a un prisma rectangular de lado derecho como a un prisma unilateral cuadrado derecho. El término prisma uniforme puede utilizarse para un prisma recto con lados cuadrados, ya que tales prismas están en el conjunto de poliedros uniforme.

Un prisma de n caras laterales con extremos de polígonos regulares y caras rectangulares, se acerca un sólido cilíndrico cuando n tiende a infinito.

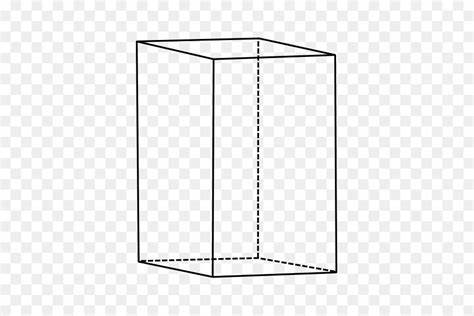
Los prismas rectos con bases regulares y longitudes iguales bordes forman una de las dos series infinitas de poliedros semirregulares, las otras series son los antiprismas.

El dual de un prisma recto es una bipirámide.

Un paralelepípedo es un prisma de que la base es un paralelogramo, o equivalentemente un poliedro con seis caras que son todas paralelogramos.

A un prisma rectangular recto también se lo conoce como cuboides, o informalmente caja rectangular. Un prisma cuadrado derecho es simplemente una caja cuadrada, y también puede ser llamado un cuboide cuadrado.Los prismas son poliedros que constan de dos caras iguales y paralelas llamadas bases, y de caras laterales que son paralelogramos.

Cada prisma consta de los siguientes elementos:

El volumen de un prisma es el producto del área de la base por la distancia o altura entre las dos bases. Su valor se expresa como:

donde B es el área de la base y h es la altura. El volumen de un prisma, cuya base es un polígono regular de n lados con una longitud de lado s, es:

El grupo de simetría de un prisma recto de n lados con la base regular es D_nh del orden 4n, excepto en el caso de un cubo, que tiene el grupo de simetría octaédrica más grande, del orden 48, que tiene como subgrupos tres versiones de D_4h. El grupo de rotación es D_n del orden 2n, excepto en el caso de un cubo, que tiene el grupo O de simetría más grande del orden 2₄, que tiene como subgrupos tres versiones de D₄.

El grupo de simetría D_nh contiene inversión si n es par.

Un politopo prismático es una generalización de los prismas a dimensiones distintas de 3. Un polítopo prismático de n dimensiones se define recursivamente como una figura creada a partir de dos politopos congruentes (n − 1)-dimensionales en hiperplanos paralelos, cuyas facetas correspondientes se conectan por prismas (n − 1)-dimensionales.

Dado un n-politopo con f_i elementos de dimensión i (i = 0, ..., n), el prisma generado a partir de él tendrá 2f_i + f_i−1 elementos de dimensión i (tomando f₋₁ = 0, f_n = 1).

Por dimensión:

Un n-polítopo regular de representado por el símbolo de Schläfli {p, q, ..., t} puede formar un (n + 1)-polítopo prismático uniforme representado por un producto cartesiano de dos símbolos de Schläfli: {p, q, ..., t} × {}.

Por dimensión:

Los politopos prismáticos de orden superior también existen como productos cartesianos de dos politopos. La dimensión de un politopo es el producto de las dimensiones de los elementos. El primer ejemplo de esto existe en un espacio de 4 dimensiones llamado duoprisma como el producto de dos polígonos. Los duoprismas regulares se representan como {p} × {q}.

Es una parte de un prisma limitada entre la base y la sección originada por un plano no paralelo a la base y que interseca a todas las aristas laterales.^[3]​

---